Relative Risk Reduction vs Absolute Risk Reduction

And understanding how clinical trials can be deceptive.

Edit 8.23.2024: This post initially mixed up “relative risk” with “risk reduction” when using the acronym RR below. Please note that the correct term is “relative risk”, which has been corrected below.

Note (6/17/2022): I have updated this post to remove the comment about my inability to figure Substack out. I have shifted this publication into my "Mini Lessons” section but it will still appear on the home page. Just a heads up.

And as always, I greatly appreciate the support that you all have shown to this Substack. It takes a lot of time and effort into writing these publications. Please consider becoming a subscriber (free or paid) and sharing my work. It means a great deal!

---

Risky Business

Let’s create a hypothetical scenario and say that you find out your predisposed to heart attacks.

Your doctor regales you with stories of this new phenomenal pill intended to reduce heart attacks. As you try to disregard all the pharmaceutical stickers plastered on the background cabinets the doc tells you that, in the clinical trials testing this drug, this amazing drug reduced the risk of heart attacks by nearly 50% in those who were given it.

That sounds phenomenal! You decide to take it, and you once again ignore the possible kickback your doctor is receiving.

But you’re also a very naughty patient, and you decide to do something blasphemous- you do your own research! In doing so, you find out that your rare genetic mutation may predispose you to heart attacks, but on an annual basis your heart attack risk may be around 0.01%.

That’s pretty low, actually really low! After finding this information, you begin to stare at that new heart medication, wondering what exactly that 50% risk reduction mean when your annual risk is around 0.01% (note that these are fake numbers- please don’t ascribe them to actual diseases).

Risk Reduction Variables

RRR vs ARR

Many clinical trials conduct their studies on the basis of poor outcomes. For heart medications, they may measure how often the treatment group suffers a heart attack compared to the placebo group. In cases where a medication such as a statin is intended to reduce cholesterol, researchers may measure how much cholesterol is reduced in the treatment group vs the placebo group. Either way, the intent is to examine if the intervention worked better than either nothing or what’s already available.

In the case of COVID vaccine trials, researchers measured the risk of symptomatic infection via PCR testing in vaccine recipients vs placebo recipients.

This type of measurement is what’s called a Relative Risk Reduction, or RRR. Relative here is the opportune word, because these risk reduction measurements compare the outcomes in the treatment group to the placebo group; essentially, how did the treatment group fare relative to the placebo group.

In more technical terms, RRR can be defined as follows¹:

Relative risk reduction (RRR) tells you by how much the treatment reduced the risk of bad outcomes relative to the control group who did not have the treatment.

Remember that relative risk reduction is different than relative risk. Relative risk is a measure that directly compares the outcomes in both the treatment and the placebo group without looking at the net reduction. In some studies risk reduction is instead referred to as a hazard ratio (HR):

The relative risk (RR) of a bad outcome in a group given intervention is a proportional measure estimating the size of the effect of a treatment compared with other interventions or no treatment at all. It is the proportion of bad outcomes in the intervention group divided by the proportion of bad outcomes in the control group.

RR takes the percentage outcome in the treatment group and divides it by the percentage outcome in the placebo group. Generally, a number higher than 1 indicates that the treatment led to worse outcomes (higher risk) while a value lower than 1 indicates that the treatment led to better outcomes (lower risk).

But let’s return to RRR. Let’s take our initial heart medication scenario and propose our own fake clinical trial.

Say that a group of 2000 people were asked to sign up for a clinical trial to test that new heart medication that reduces heart attacks in those with a rare genetic mutation.

One thousand goes into the treatment group, one thousand goes into the placebo group.

Each group is provided a daily intervention (treatment or placebo) and the researchers measure the incidences of heart attacks among each group over the course of 6 months.

Now, let’s look back at that 50% reduction we started with at the top of the article. Half off of anything is phenomenal, but with anything we need context to properly examine the numbers.

At the end of the 6 months the results of the trial found that one person in the treatment group suffered a heart attack while two people in the placebo group did.

If we were to conduct an RRR, we would need to first find the percentage of participants who had bad outcomes². Using the numbers from our hypothetical study:

• Placebo group: 2/1000 = 0.002

  • Multiply 0.002 by 100 to turn it into a percentage gives us

  • 0.002 * 100 = 0.2%

• Treatment Group: Following the same equations, we should get a percentage of 0.1% for the treatment group.

Next, we would have to take the difference between the two by subtracting the treatment group from the placebo group.

• Placebo% - Treatment% = % Difference (i.e. the ARR, described in more context further down)

• In the case of this hypothetical study:

  • 0.2% - 0.1% = 0.1%

And lastly, this net difference must be divided by the percentage of outcomes in the placebo group in order to get the RRR. Remember that we still need to multiply this number by 100 to turn it back into a percentage.

• % Difference / Placebo%

• 0.1% / 0.2% = .5

• Then multiplying by 100 to get the RRR percentage

  • .5 * 100 = 50% RRR

So there we have that 50% reduction. Again, alone it would look great, but within the context of this fake study it may not mean much.

If we look at the placebo group, 2 in 1000 patients suffered a heart attack. Percentage-wise that’s 0.2% of participants (2/1000), which is a very low number.

In the treatment group, 1 in 1000 translates to 0.1% of participants (1/1000) suffering a heart attack.

Both of these numbers by themselves are very low- both groups aren’t suffering from heart attacks to any substantial degree. But in order to compare the groups, if we take 0.2% from the placebo group and the 0.1% from the treatment groups, we get a net difference of 0.1%.

0.2% (placebo) - 0.1% (treatment) = 0.1% ARR

What does that mean?

That means that 0.1% of the population who takes this new heart medication may see a reduction in heart attacks over the span of 6 months- essentially, almost no real-world reduction.

This risk reduction calculation is what’s called Absolute Risk Reduction (ARR), and it’s the most valuable of the two risk reduction measures for the main fact that it takes into account the real world utility of a medication or therapy.

A drug may purport to reduce cancer by a substantial amount compared to older treatments (RRR), but if the older treatments are considered to be predominately ineffective anyways then the actual effect size of this new cancer drug may be low (ARR): cancer patients may still have poor outcomes on this new drug even if it is better than older drugs.

In essence, RRR may lead to an over exaggeration of a drug’s actual effectiveness. It may suggest some mathematical significance while the actual clinical, real-world significance may be much smaller.

Overall, ARR is a more desirable measure of outcomes while RRR may lead to deceptive conclusions (Ranganathan, et. al.):

Physicians tend to over-estimate the efficacy of an intervention when results are expressed as relative measures rather than as absolute measures.[2] ARR (expressed along with baseline risk) is probably a more useful tool than RRR to express the efficacy of an intervention.[3] Thus, reporting of absolute measures is a must. The CONSORT statement for reporting of results of clinical trials recommends that both absolute and relative effect sizes should be reported.[4] It helps to report NNT in addition, since this is an easily-interpreted single indicator of clinical utility of an intervention.

Compare the hypothetical outcomes in the below table and see how they alter the ways that both ARR and RRR are interpreted:

From Ranganathan, et. al. Note that both the 1st and 4th row show the same RRR values, yet different ARR values. The 4th column likely shows a lower treatment effect size than the 1st column in this hypothetical scenario. Results like the 4th row may be considered not clinically significant, even though the RRR may suggest otherwise. Refer to the equations at the top as a general guidance for these calculations.

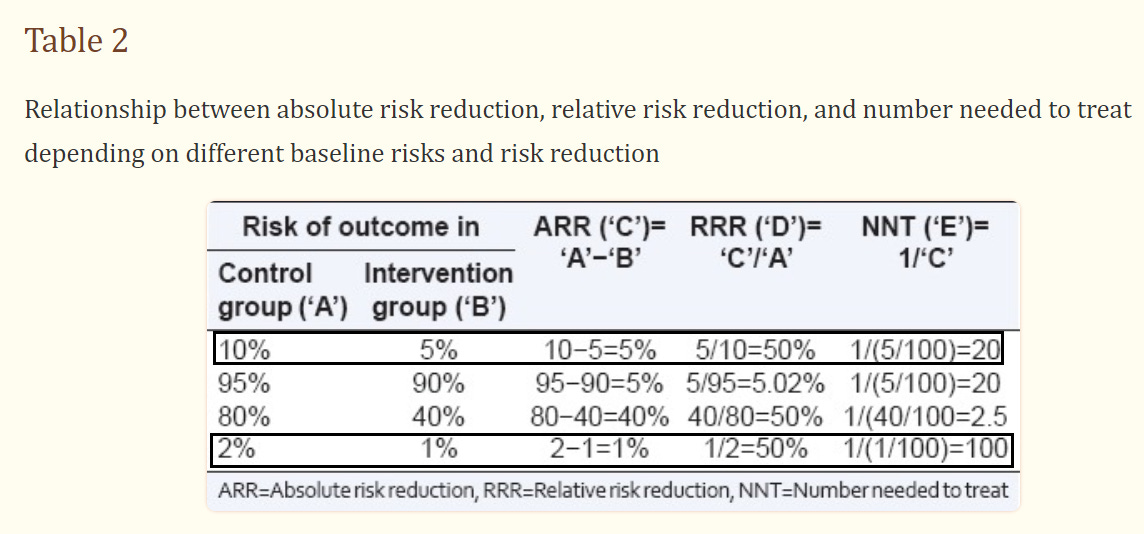
We can see how clinical trials reporting only on RRR can end up rather deceptive by missing out on real world factors. It also explains why miraculous drugs may end up actually failing when brought to market.

Number Needed to Treat (NNT)

The last thing I cover before providing real-world examples will be this term called Number Needed to Treat (NNT).

If you provide millions of people a drug, you may not worry about percentages. People aren’t, in fact, percentages. Instead, you may want to see how many actual people will benefit from the drug.

Sometimes you only need to give a few people a therapy in order to see one or two people improve. Other times you may need to prescribe the drug to thousands of patients in order to see one benefit.

NNT is a measure of how many people must be given a treatment before at least 1 may see the benefits.

Its calculation takes 1 and divides in by the ARR value (1/ARR).

In the above table you can see that an ARR of 5% provides an NNT of 20, suggesting that 20 people need to receive the treatment before 1 can be considered to have benefited. And it makes sense, since that value is extrapolated from that ARR of 5%.

When the ARR is 1%, then 100 people (NNT=100) need to be given a treatment for at least 1 to benefit.

When the ARR is 0.1%, like in our fake heart medication trial above, then the NNT is 1,000 and means 1,000 people must be given a treatment for at least 1 person to benefit.

Essentially, NNT is a corresponding measure of ARR that highlights how the fewer people benefit from a treatment the more people must receive the treatment in order to see some noticeable effect size. A good end result for pharmaceutical companies, if I must say so.

So with this information in mind, let’s consider a few real-world scenarios and understand how clinical trials can obfuscate the actual real world benefits of drugs, much to the harm of the consumer.

Real-World Examples

Statins and the JUPITER Trial

In 2008 one of the largest statin studies ever conducted was released and met with much fanfare.

The study, named the Justification for the Use of Statins in Primary Prevention: An Intervention Trial Evaluating Rosuvastatin (JUPITER) trial, was intended to be a 5 year longitudinal study that looked at the effects of daily statin intake (Rosuvastatin, brand name CRESTOR- given 20 mg/day) in participants who had relatively healthy cholesterol levels. The end-goal was to see if daily statin intake would reduce incidences of cardiovascular disease and cardiac events such as heart attacks, strokes, or death (primary end point). Note that this study was not necessarily a measure of cholesterol reduction, but a measure of the inferential effects of high cholesterol.

The study was sponsored by the drug manufacturer AstraZeneca, and it enrolled 17,802 participants. However, the trial was stopped short of the 2 year mark, with the researchers remarking that the results were so good that the study did not need to be conducted any further (from the clinicaltrials.gov page of the JUPITER trial):

AstraZeneca announced it has decided to stop the CRESTOR JUPITER clinical study early based on a recommendation from an Independent Data Monitoring Board and the JUPITER Steering Committee, which met on March 29, 2008. The study will be stopped early because there is unequivocal evidence of a reduction in cardiovascular morbidity and mortality amongst patients who received CRESTOR when compared to placebo.

On the surface, the results would seem phenomenal. The primary end point measures indicated 142 incidences in the statin group vs 251 in the placebo group- a risk reduction (or hazard ratio, as measured in these trials) of about 0.56, or an RRR of about 44%. Again, on the surface these results would be phenomenal!

However, fallout and criticism began to arise in regards to this trial. Questions were raised as to the actual clinical significance of the trial and whether it was ended too soon.

Dr. Mark Hlatky³ released an editorial in which he raises questions about the absolute risk reduction of the study- the more clinically significant piece:

The relative risk reductions achieved with the use of statin therapy in JUPITER were clearly significant. However, absolute differences in risk are more clinically important than relative reductions in risk in deciding whether to recommend drug therapy, since the absolute benefits of treatment must be large enough to justify the associated risks and costs. The proportion of participants with hard cardiac events in JUPITER was reduced from 1.8% (157 of 8901 subjects) in the placebo group to 0.9% (83 of the 8901 subjects) in the rosuvastatin group; thus, 120 participants were treated for 1.9 years to prevent one event [NNT].

And similar sentiments were raised in an editorial by Vaccarino, et. al.⁴ (emphasis mine):

The reason for the enthusiasm and early termination of JUPITER was a hazard ratio of 0.56 (95% CI, 0.46 to 0.69), translating into a 44% relative risk reduction for the primary outcome favoring statin treatment, with similar reductions in other cardiovascular endpoints. But as Dr. Hlatky cautioned, in his editorial to the JUPITER trial,5 what really matters for dictating changes in clinical practice is the absolute risk reduction. This is because the absolute benefit of the treatment must be large enough to justify its potential risks and costs. Importantly, the threshold for tolerating risks and costs are particularly low when dealing with predominantly healthy populations who have low event rates, such as the sample enrolled in JUPITER. The question therefore is: are the treatment benefits achieved in the JUPITER trial large enough to advocate an expansion in the clinical indications for statins? […]

The rate of the primary end point, a composite of five conditions (nonfatal myocardial infarction, nonfatal stroke, hospitalization for unstable angina, arterial revascularization, or confirmed death from cardiovascular causes) was only 0.77% per year in the rosuvastatin arm and 1.36% in the placebo arm. These rates translate into an absolute risk reduction of about a half percentage point per year (0.59%), or 1.2% over the approximately 2-year total duration of the trial. This figure is obviously much less impressive to the casual reader than the relative risk reduction of 44%. If one considers the more important and customary outcome of major coronary events, including nonfatal or fatal myocardial infarction, the yearly rate in the two arms was 0.17% and 0.37% respectively, yielding an absolute risk reduction of only 0.20% per year. However, the corresponding relative risk reduction remained an impressive 54%. When dealing with low event rates, even a small absolute difference in rates can appear dramatic when expressed in relative terms (e.g., as a hazards ratio, or relative risk reduction).

And so there have been quite a few criticisms in regard to statins. What is the actual clinical significance, and what are the actual takeaways from these studies?

Considering that statins are one of the most highly prescribed medications, shouldn’t we as consumers be informed as to whether the drugs we take actually provide any sort of benefit, rather than obfuscating the actual facts through number manipulation?

But in essence, it’s the reporting of these RRR values in studies that provide some allurement to both doctors and patients, with pharmaceutical manufacturers relying on the inability for the layperson and those in the medical field to be able to discern these differences (Vaccarino, et. al.):

Because JUPITER was an industry-sponsored trial, readers should be cognizant of potential marketing interests when evaluating the trial results; interests may not necessarily align with public health goals.16 The strategy of stopping the trial early and the choice of presenting relative rather than absolute effect estimates are in line with the industry goals of disseminating the results quickly and in the most favorable way, therefore maximizing potential profits, while at the same time minimizing research costs. Promoting the use of drugs for healthy people, an enormous potential market, is a powerful business strategy for pharmaceutical corporations in need of showing sustained profit growth to their share holders and seeking to extend the life of their patents. Medical professionals should be aware of the commercial implications of industry-sponsored trials, which unfortunately represent the majority of contemporary drug trials. A bias related to industry sponsorship has been previously demonstrated in the presentation of trial results.17, 18 Thus, it is imperative to carefully and critically evaluate the data generated by industry-sponsored trials, since these data remain the cornerstone of evidence-based medicine and practice guidelines.

Pfizer COVID Vaccine

Since we are currently in the grips of COVID vaccine hysteria, it would be good to see how these same issues in RRR presentation can lead to misleading conclusions from these COVID vaccine trials.

We should be a bit familiar with these vaccine trials, so I’ll skip to the study measurements. Our focus will be on the Pifzer trial⁵, because why not? I don’t mind picking on Pfizer anyways.

Fortunately, Pfizer provided us a table to look at:

When I first saw this study more than a year ago I wasn’t quite sure where they got their 95% vaccine efficacy from, but note that vaccine efficacy is actually referring to relative risk reduction (RRR) here.

If we do a bit of number crunching we can come up with their results. Try it for yourself and follow along with the process. I’ll be using the numbers from the first row of the table to calculate the RRR.

1. Divide the number of infected participants in each group by their corresponding participant number (the N= value). *As a heads up, note that you don’t have to keep multiplying by 100, but can instead use the original values (not the percentage values) and then just convert the value into a percentage at the end. This is because the percentages will just cancel themselves out during each calculation. I will be doing this here, although I will include the percentage on the side for later.

   1. For the Vaccine group: 8 / 18,198 = 0.000496, or 0.0496%

   2. For the Placebo group: 162 / 18,325 = 0.00884, or .884%

2. Find the difference between the two groups.

   1. Placebo ratio - Vaccine ratio

   2. 0.00884 - 0.000496 = 0.00834

3. Divide this difference found in #2 by the Placebo value from #1. Then multiply by 100 at the last step to get the % RRR.

   1. Difference / Placebo

   2. 0.00834 / 0.00884 = 0.944

   3. 0.944 * 100 = 94.4% RRR

My number is slightly off- mostly because of the significant digits used in the calculations, but understand that you should get a number pretty close to 95% if you followed the calculations through properly.

So we can see how Pfizer and these researchers were able to come up with this 95% vaccine efficacy and wow the world with such phenomenal results. But of course, you are smarter than that now, and you know that we need to look at the absolute risk reduction to see a real-world effect.

In order to do that, we just need to take the percentage values from #1 of the calculation that I left on the side, take their difference. I’m using the percentage value here since we aren’t dividing and having to worry about cancelling out units or other values.

• .884% - 0.0496% = 0.8344% ARR

Again, your numbers may vary but you should at least be slightly below 1%. And what does that mean?

It means that, at least at the time that this study was conducted, that your absolute risk reduction from being infected by COVID after vaccination is around 0.8%.

Yes, a measly .8% risk of overall infection reduction. Now, keep in mind, as I noted in my vaccinology series, that transmission rate and viral virulence will alter this number. This number is likely not accurate in the Omicron era.

But nonetheless, we can see that there’s such a drastic difference between RRR and ARR in the context of these vaccines. We can also understand why no ARR value was provided.

But the most important assessment of these numbers is understanding what they mean in context, and why there’s such a wide discrepancy between the two.

For one, if we look at the original percentages from #1 of the calculation we can see that, in general, the risk of infection in both groups was already extremely low. In both groups it was already below 1% risk of infection.

Because these were already at such small numbers, calculations of relative effect size such as RRR are likely to over exaggerate the actual effect.

Remember the line from the Vaccarino, et. al. excerpt above:

When dealing with low event rates, even a small absolute difference in rates can appear dramatic when expressed in relative terms (e.g., as a hazards ratio, or relative risk reduction).

Essentially, small numbers can be made to look big with a bit of manipulation. This is even made more clear when looking at some of these vaccine clinical trials which show 100% efficacy in reducing hospitalization and death. It’s easy to tout such numbers when only a few dozen people in a placebo group greater than 10,000 require hospitalization or die.

It’s interesting that The Pfizer clinical trial had this minor comment in the Discussion section (Polack, et. al.):

The vaccine met both primary efficacy end points, with more than a 99.99% probability of a true vaccine efficacy greater than 30%. These results met our prespecified success criteria, which were to establish a probability above 98.6% of true vaccine efficacy being greater than 30%, and greatly exceeded the minimum FDA criteria for authorization.9

Note the wording here, which somewhat glosses over the fact that the actual primary endpoint of the study was a vaccine efficacy (RRR) over 30%. Not much of a threshold to climb over, quite honestly.

But even disregarding this absolutely low ARR value, there are plenty of criticisms of these trials, and whether they accurately reflect any effectiveness of these vaccines at all.

Instead, this use of the RRR as a vaccine efficacy number is used as a marketing tactic that encouraged people to get vaccinated. Why wouldn’t someone want something with a 95% efficacy rate? It’s an obfuscation of any real-world, clinical significance in order to push for the mass administration of something which, at the time, had no long-term safety data.

Driving without a vaccine

Many people like to compare the vaccines to driving without a seatbelt. It’s why I mentioned it in last Friday’s post. Seatbelts are great, but they theoretically only work at the time of impact- when you actually get into a car accident.

For many of us who may mind the speed limit and provincial traffic laws, we may not get into accidents all that much (if we do at all).

Now, I do hope that people at least wear their seatbelts, but if we hardly ever get into an accident do we really care about whether the seatbelt saves us?

And this is the main problem with these COVID vaccines. They are only effective in the moment that we come into contact with the virus. Such clinical trials cannot provide any contextual information on stress-testing because no researcher would be able to accurately predict or determine how someone who is vaccinated behaves.

The researchers may hope that just the mere act of vaccination, whether with the actual vaccine or a saline shot, may lead trial participants to become a little more free-spirited and increase their chances of exposure. But that’s not always the case, and it’s certainly not the case when messaging discouraged social interactions and when most people were still locked away in their homes.

These vaccines needed to have been stress-tested during clinical trials. They require that people be exposed to the pathogen in order to test if someone is protected from said pathogen. It’s the reason why car manufacturers smash their vehicles into walls with the hope that their test dummies don’t go flying out the front window.

But because of these many faults, people were likely not provided adequate information, and instead were made to rely on the faulty 95% vaccine efficacy number that really meant nothing in a real-world setting.

---

Hopefully this has helped you understand the difference between relative risk reduction and absolute risk reduction. When viewing the results of any clinical trial keep an eye out and see which value is presented to you as a viewer and customer. Are you provided all of the nuances of the trial and what all of the values mean? Or will you be slapped with some hazard ratio or risk reduction and are told to assume that this number means something important.

Know that you’re a lot more intelligent than that, and learn to stop taking these numbers at face value. Pharmaceutical companies rely on marketing tactics just as much as your favorite cookie company, and so don’t fall for the numbers.

Then you’ll become a more informed consumer.

1. Irwig L, Irwig J, Trevena L, et al. Smart Health Choices: Making Sense of Health Advice. London: Hammersmith Press; 2008. Chapter 18, Relative risk, relative and absolute risk reduction, number needed to treat and confidence intervals. Available from: https://www.ncbi.nlm.nih.gov/books/NBK63647/

Ranganathan, P., Pramesh, C. S., & Aggarwal, R. (2016). Common pitfalls in statistical analysis: Absolute risk reduction, relative risk reduction, and number needed to treat. Perspectives in clinical research, 7(1), 51–53. https://doi.org/10.4103/2229-3485.173773

2. As I’ll explain when examining the Pfizer COVID vaccine trial, you don’t necessarily need to keep calculating your values into percentages. The most important time will likely be at the end, as doing it throughout will just lead to the calculations cancelling themselves out.

3. Hlatky M. A. (2008). Expanding the orbit of primary prevention--moving beyond JUPITER. The New England journal of medicine, 359(21), 2280–2282. https://doi.org/10.1056/NEJMe0808320

4. Vaccarino, V., Bremner, J. D., & Kelley, M. E. (2009). JUPITER: a few words of caution. Circulation. Cardiovascular quality and outcomes, 2(3), 286–288. https://doi.org/10.1161/CIRCOUTCOMES.109.850404

5. Polack, F. P., Thomas, S. J., Kitchin, N., Absalon, J., Gurtman, A., Lockhart, S., Perez, J. L., Pérez Marc, G., Moreira, E. D., Zerbini, C., Bailey, R., Swanson, K. A., Roychoudhury, S., Koury, K., Li, P., Kalina, W. V., Cooper, D., Frenck, R. W., Jr, Hammitt, L. L., Türeci, Ö., … C4591001 Clinical Trial Group (2020). Safety and Efficacy of the BNT162b2 mRNA Covid-19 Vaccine. The New England journal of medicine, 383(27), 2603–2615. https://doi.org/10.1056/NEJMoa2034577